Set Theory in Typescript

Set theory is a branch of mathematical logic that deals with the study of sets, which are collections of distinct objects. Set theory is concerned with understanding the properties and relationships between sets, including their size, intersection, union, and complement. The study of set theory has many applications in mathematics, computer science, linguistics, and philosophy.

In simple terms - Set Theory tells you about the relationships between distinct groups of items. If you are interested in a detailed description check out wikipedias article on set theory.

How to use Set Theory in Typescript

All examples will make use for the following simple Sets.

// Base Sets to use for our types
const one = new Set([1,2,3,4] as const)
const two = new Set([3,4,5,6] as const)

Union - A ∪ B

In set theory, a union of sets is a new set that contains all the distinct elements that are in at least one of the original sets. This can be extended to as many sets as you wish to include, but in this case I will have all examples use two sets to keep thins simple.

As you can see from the diagram everything is highlighted in colour - meaning all the values should be represented in the final set.

To represent this in Typescript there are two parts.

1. Implementing a function that will return the correct Set values.
2. Creating the Types so that the Types are represented correctly.

Implementation

For a union we simple take the existing values from both Sets and pass them in to a new Set constructor. The Set structure will ignore any duplicates for us.

// As a reusable function
function Union(one: Set<any>, two: Set<any>) {
  return new Set([...one, ...two]);
}

Union(one, two); // Type is `Set<any>`

Type

The problem with the basic implementation above is that we do not have any valuable type information when we use it. Using setOne and setTwo above results in a Set<any> type.

We can use generics to pass through our types in a more detailed way.

// Add types `T` and `U`
function Union<T, U>(one: Set<T>, two: Set<U>) {
  return new Set([...one, ...two]);
}

Union(one, two); // Type is `Set<1|2|3|4|5|6>`

Just like that we now have our returned type as Set<1|2|3|4|5|6> - so Typescript knows what our new set contains.

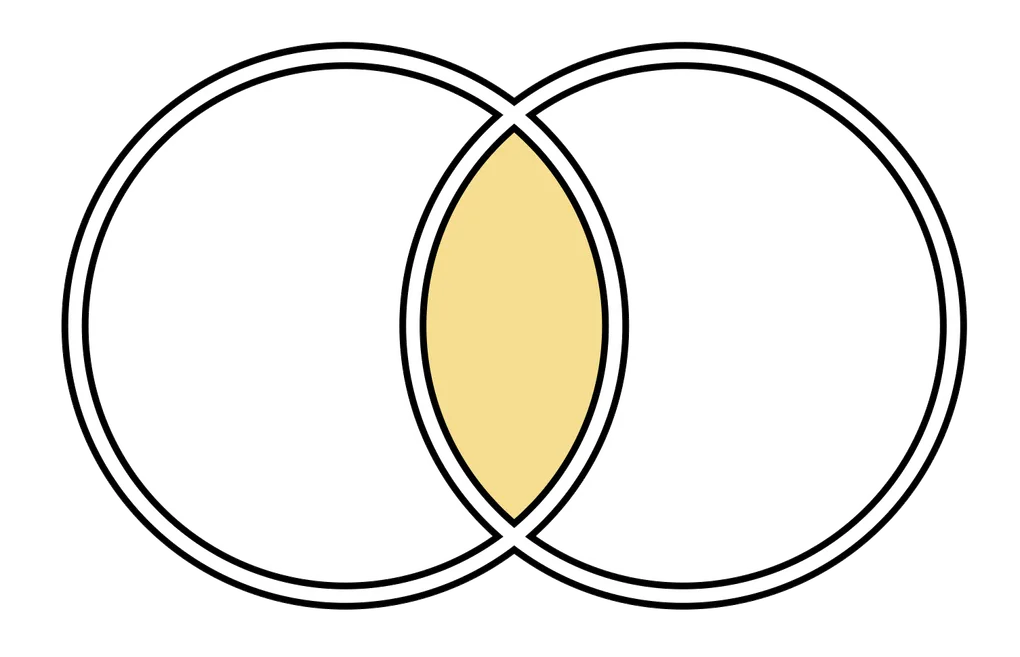
Intersection - A ∩ B

Set intersection is a basic operation in set theory that involves finding the common elements between two or more sets. The result of a set intersection operation is a new set that contains only those elements that are present in all the sets being intersected.

In the diagram above, only the inner part of the sets are highlighted. What this means is that only the elements that are in both sets are in the final set.

Implementation

For in intersection, we want to create a new set from the values of the first Set and filter out any that are not in the other Sets.

// NOTE: The same generics from Union have been kept
function Intersection<T, U>(one: Set<T>, two: Set<U>) {
  // only values that are in both sets
  return new Set([...one].filter(x => two.has(x)));
}

Intersection(one, two); // Type is `Set<1 | 2 | 3 | 4>`

This time even with the generics added the result type is not what is expected. Typescript figured out that the values should be limited to what is in Set one, but failed to identify what the filter does.

Type

To fix this functions type, we need to let Typescript know what the filter function is going to return. Fortunately filter comes with a generic option to specify the result. We can use that to make sure that T is also a member of U.

function Intersection<T, U>(one: Set<T>, two: Set<U>) {
  // New type that is the intersection of T and U
  type Intersection = T extends U ? T : never;

  // Pass the type into filter
  return new Set(
    [...one].filter<Intersection>(x => two.has(x))
  );
}

Intersection(one, two); // Type is `Set<3 | 4>`

Difference - A - B

Set difference is an operation in set theory that determines the elements that are present in one set but not in another. The result is the set of all elements that are in A but are not in B.

This is known as the Relative Complement of B in A.

In the diagram above, only the left side is highlighted. What this means is that values that are in setOne and not in setTwo are in the result. Flipping the sets B - A would mean only the right side is highlighted.

Implementation and Type

This is a similar operation to Intersection, but we just need to flip the condition for both the implementation and the type.

function Difference<T, U>(one: Set<T>, two: Set<U>) {
  // Flipped `never` and `T` in the ternary
  type Difference = T extends U ? never : T;

  // add a NOT before `two.has(X)`
  return new Set([...one].filter<Difference>(x => !two.has(x)));
}

Difference(one, two); // Type is `Set<1 | 2>`

Symmetric Difference - A △ B or (A-B) ∪ (B-A)

The symmetric difference of two sets A and B is the set of elements that are in either A or B, but not in their intersection. In other words, it is the set of elements that are in exactly one of the two sets.

The diagram above shows the left and right being highlighted, and the middle not, making the diagram symmetric.

Implementation and Type

The symmetric difference is just the difference of A - B and B - A combined so we can use the existing difference function twice to find it.

function SymmetricDifference<T, U>(one: Set<T>, two: Set<U>) {
  // Combine `A - B` and `B - A`
  return new Set([
    ...Difference(one, two),
    ...Difference(two, one)
  ]);
}

SymmetricDifference(one, two); // Type is `Set<1 | 2 | 5 | 6>`

Conclusion

In this article, we have explored the fundamental operations of set theory: union, intersection, and complement. These operations provide a powerful toolset for manipulating sets and analyzing their properties. By combining these operations, we can create complex sets and express a wide range of mathematical concepts.

What to read more? Check out more posts below!